
‚Nicht wissen‘ und ‚Nicht-Wissen‘. Begriffsanalytische und sprachpragmatische Betrachtungen
von Wolfgang Lenzen (Osnabrück)
Im Alltag passiert es allzu häufig, dass wir etwas, das andere von uns wissen wollen, leider nicht wissen:
- „Wo sind die Wagenschlüssel?“ – „Ich weiß es nicht!“
- „Wer war der Mann gerade, der uns zugelächelt hat?“ – „Ich weiß es nicht!“
- „Wann beginnen in Niedersachsen 2020 die Sommerferien?“ – „Ich weiß es nicht!“
- „Wie heißt der gegenwärtige Ministerpräsident von Polen?“ – „Ich weiß es nicht!“ …
In gewisser Weise gilt für jeden von uns, dass unser Nicht-Wissen unser Wissen quantitativ weit übertrifft. Im Folgenden soll dieses Nicht-Wissen begriffslogisch näher analysiert werden. Dazu ist es unabdingbar, zunächst den positiven Begriff des Wissens zu präzisieren, und dieses setzt wiederum voraus, auch das Verhältnis von Wissen und Glauben zu klären.
Im angelsächsischen Sprachraum lauten die zentralen Verben ‚to know‘ und ‚to believe‘. Entsprechend verwendet man dort fast ausschließlich jene Substantive, die den Titel für das bahnbrechende Werk von J. Hintikka aus dem Jahre 1962 lieferten: Knowledge and Belief. Genauer benutzt Hintikka neben den standardisierten Ausdrücken ‚a knows that p‘ und ‚a believes that p‘, die er durch Kap und Bap abkürzt, noch zwei weitere Formeln Pap und Cap, die – in nicht sonderlich idiomatischer Weise – als ‚it is possible, for all that a knows, that p‘ bzw. als ‚it is compatible with everything a [believes] that p‘ paraphrasiert werden. Wie sich im weiteren Verlauf seiner Introduction to the Logic of the Two Notions zeigte, sind die Formeln Pap und Cap jedoch definierbar und brauchen deshalb nicht als zusätzliche Grundoperatoren betrachtet zu werden.
Im Folgenden weichen wir von Hintikkas Symbolismus leicht ab und benutzen W(a,p) und G(a,p) als Abkürzungen für ‚a weiß, dass p‘ bzw. ‚a glaubt, dass p‘. Außerdem verwenden wir die logischen Symbole für die Operatoren der Negation („¬“ für „nicht“), der Konjunktion („∧“ für „und“), der Disjunktion („∨“ für „oder“), der (logischen) Implikation („→“ für „wenn, dann“) sowie der (logischen) Äquivalenz („↔“ für „genau dann, wenn“).
Epistemisch-doxastische Grundbegriffe
Im deutschen Sprachraum ist es geläufig, neben der im eigentliche Sinne epistemischen Einstellung ‚a weiß, dass p‘ (griech. episteme = Wissen) drei weitere doxastische Einstellungen (griech. doxa = Meinung, Glaube) zu unterscheiden:
- a ist davon überzeugt, dass p Ü(a,p)
- a glaubt, dass p G(a,p)
- a hält es für möglich, dass p M(a,p).
Mit dem Instrumentarium der Theorie subjektiver Wahrscheinlichkeit könnte man Ü(a,p) dahingehend präzisieren, dass eine feste Überzeugung dann und nur dann vorliegt, wenn die Aussage p für die Bezugsperson a die maximale Wahrscheinlichkeit 1 besitzt. Für den schwächeren Begriff G(a,p) wäre hingegen nur zu fordern, dass p für a wahrscheinlicher ist als das Gegenteil, ¬p. Mit anderen Worten: a glaubt nur dann, dass p, wenn p für a eine Wahrscheinlichkeit größer als ½ besitzt. Schließlich lässt sich der Operator M(a,p) probabilistisch so deuten, dass a die Aussage p dann und nur dann für möglich hält, wenn p für a eine Wahrscheinlichkeit größer als 0 besitzt.
Aufgrund dieser Deutung – aber auch unabhängig von ihr – gelten die folgenden logischen Beziehungen: Ü(a,p) → G(a,p) → M(a,p), d.h. wenn jemand davon überzeugt ist, dass p, dann glaubt er auch, dass p, und erst recht hält er es für möglich, dass p. Denn wenn p für a die Wahrscheinlichkeit 1 besitzt, dann ist diese größer als ½ und also erst recht größer als 0. Ferner gelten aufgrund der probabilistischen Deutung – aber auch unabhängig von ihr – die folgenden Äquivalenzen, die es gestatten würden, einen der Begriffe Ü(a,p) oder M(a,p) wahlweise durch den anderen zu definieren:
(Ü1) Ü(a,p) ↔ ¬M(a,¬p)
(M1) M(a,p) ↔ ¬Ü(a,¬p).
Jemand ist also dann und nur dann davon überzeugt, dass p, wenn er es nicht für möglich hält, dass nicht-p, bzw. umgekehrt: jemand hält es dann und nur dann für möglich, dass p, wenn er es nicht für ausgeschlossen hält, dass nicht-p. Schließlich gilt aufgrund der probabilistischen Deutung das Widerspruchsfreiheitsgesetz
(G1) G(a,p) → ¬G(a,¬p).
Denn wenn die Aussage p für a eine Wahrscheinlichkeit größer als ½ besitzt, dann muss die Wahrscheinlichkeit von ¬p für a kleiner als ½ sein, so dass a nicht zugleich glauben kann, dass ¬p. Aber auch unabhängig von unserer probabilistischen Interpretation darf man festhalten, dass im Sinne eines rationalen Glaubens niemand zugleich glauben kann, dass p der Fall ist, und dass p nicht der Fall ist.
Wie in Lenzen (2012) gezeigt wurde, lassen sich die logischen Beziehungen zwischen den verschiedenen doxastischen Einstellungen durch ein doppeltes, ineinander geschachteltes „logisches Quadrat“ darstellen:
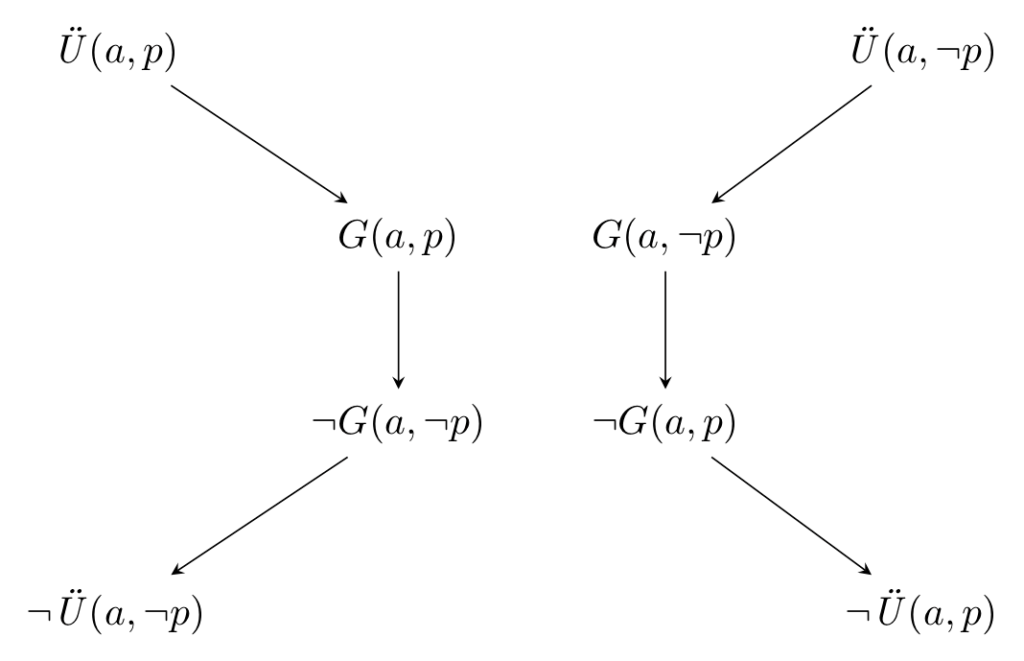
Nach Parsons (2017) lassen sich dabei die generellen Eigenschaften eines „Square of Opposition“ wie folgt zusammenfassen.
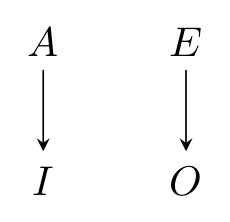
Die Sätze in der oberen Reihe (A und E) sind konträr zueinander, d.h. sie können auf keinen Fall zusammen wahr, wohl aber zusammen falsch sein. Die diagonal gegenüberliegenden Sätze (also A und O einerseits, sowie E und I andererseits) stehen sich kontradiktorisch gegenüber, d.h. sie können weder zusammen wahr, noch zusammen falsch sein. Die Sätze in der unteren Reihe (I und O) sind subkonträr, d.h. sie können nicht zusammen falsch, wohl aber zusammen wahr sein. Bereits aus diesen Festlegungen ergibt sich schon das Gesetz der Subalternation, demzufolge – wie durch die Pfeile ‚↓‘ symbolisiert – aus der oberen Aussage (A bzw. E) die jeweils darunter stehende Aussage (I bzw. O) logisch folgt.[1]
In neuerer Zeit betrachtet man gelegentlich die Erweiterung des „Square“ zu einem „Hexagon of Opposition“, bei dem zwei Aussagen U und Y hinzugefügt werden, deren eine, Y, als Konjunktion von I und O verstanden werden soll, und die andere, U, entsprechend als Disjunktion von A und E:
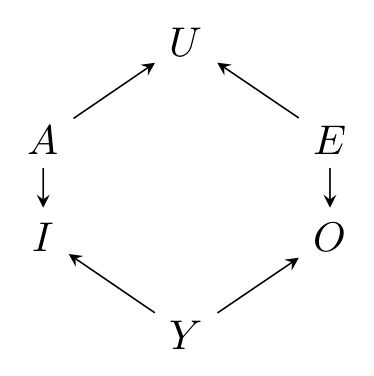
Überträgt man diesen Gedanken auf die Einstellungen des starken bzw. schwachen Glaubens, so erhält man die zusätzlichen Formeln Ü(a,p) ∨ Ü(a,¬p) und G(a,p) ∨ G(a,¬p), die zum Ausdruck bringen, dass die Person a eine (starke oder schwache) Meinung bezüglich p hat. Die Negationen, also ¬Ü(a,p) ∧ ¬Ü(a,¬p) bzw. ¬G(a,p) ∧ ¬G(a,¬p), bringen entsprechend zum Ausdruck, dass a keine (starke oder schwache) Meinung bezüglich p hat.
Wissen und Nicht-Wissen
Nach der Klärung der doxastischen Begriffe wenden wir uns nun dem eigentlichen epistemischen Begriff zu! Spätestens seit Platons klassischer Analyse des Wissens als einem „wahren, begründeten Glauben“ steht fest, dass jemand nur dann wissen kann, dass p, wenn p tatsächlich der Fall ist:
(W1) W(a,p) → p.
Außerdem kann a nur dann wissen, dass p, wenn a zugleich glaubt, dass p. Diese These gestattet eine schwächere und eine stärkere Lesart:
(W2+) W(a,p) → Ü(a,p)
(W2–) W(a,p) → G(a,p).
Durch die „Wahrheitsbedingung“ (W1) unterscheidet sich der Begriff des Wissens entscheidend von dem des Glaubens, denn selbst wenn a im höchsten Grad davon überzeugt ist, dass p, so garantiert dies noch nicht, dass p tatsächlich der Fall ist. Hintikka (1962: 48) drückte dies knapp wie folgt aus: „[…] whatever is known has to be true. There is no reason why what is believed should be true.“ Tatsächlich scheint für Hintikka die Nichtgeltung der Wahrheitsbedingung der einzige Punkt zu sein, in dem sich der Begriff des Glaubens von dem des Wissens logisch unterscheidet. Aus diesem Grunde hat er auch die Logik des Glaubens gegenüber der des Wissens ziemlich vernachlässigt.
Aus dem Operator W(a,p) kann man mit Hilfe von Negationen die weiteren Formeln W(a,¬p), ¬W(a,p) und ¬W(a,¬p) erzeugen. Dabei bringt W(a,¬p) zum Ausdruck, dass a weiß, dass nicht-p der Fall ist, bzw. dass a weiß, dass p nicht der Fall ist, während ¬W(a,p) beinhaltet, dass a nicht weiß, dass p der Fall ist. Schließlich besagt die doppelt negierte Formel ¬W(a,¬p), dass a nicht weiß, dass p nicht der Fall ist. Die vier epistemischen Ausdrücke W(a,p), W(a,¬p), ¬W(a,¬p) und ¬W(a,p) bilden offenkundig ein „logisches Quadrat“:

Zum einen sind die Formeln an den diametral gegenüberliegenden Ecken kontradiktorisch zueinander, denn ¬W(a,p) stellt ja genau die Negation, also das kontradiktorische Gegenteil von W(a,p) dar, und ¬W(a,¬p) jenes von W(a,¬p)! Ferner sind W(a,p) und W(a,¬p) konträr zueinander, d.h. sie können auf keinen Fall zusammen wahr sein. Würde nämlich zugleich gelten W(a,p) und W(a,¬p), so müsste einerseits p, andererseits aber auch ¬p der Fall sein – das ist jedoch ein trivialer logischer Widerspruch! Dass die Sätze W(a,p) und W(a,¬p) darüber hinaus zusammen falsch (und also die subkonträren Sätze ¬W(a,¬p) und ¬W(a,p) zusammen wahr) sein können, ließe sich durch viele Alltagsbeispiele illustrieren. Zum Beispiel weiß ich nicht, dass es am Montag in einer Woche in Osnabrück regnen wird; aber ich weiß auch nicht, dass es am Montag in einer Woche in Osnabrück nicht regnen wird. Generell gibt es viele Sachverhalte p, bezüglich derer ich keine feste Meinung habe, ob p oder ob ¬p eintreten wird. Deshalb gilt erst recht: Ich weiß nicht, ob p, d.h. ich weiß weder, dass p, noch weiß ich, dass nicht-p. Definiert man den Begriff des Wissens-ob in naheliegender Weise durch W(a,p) ∨ W(a,¬p), so lässt sich das epistemische Quadrat zu einem Sechseck vervollständigen:
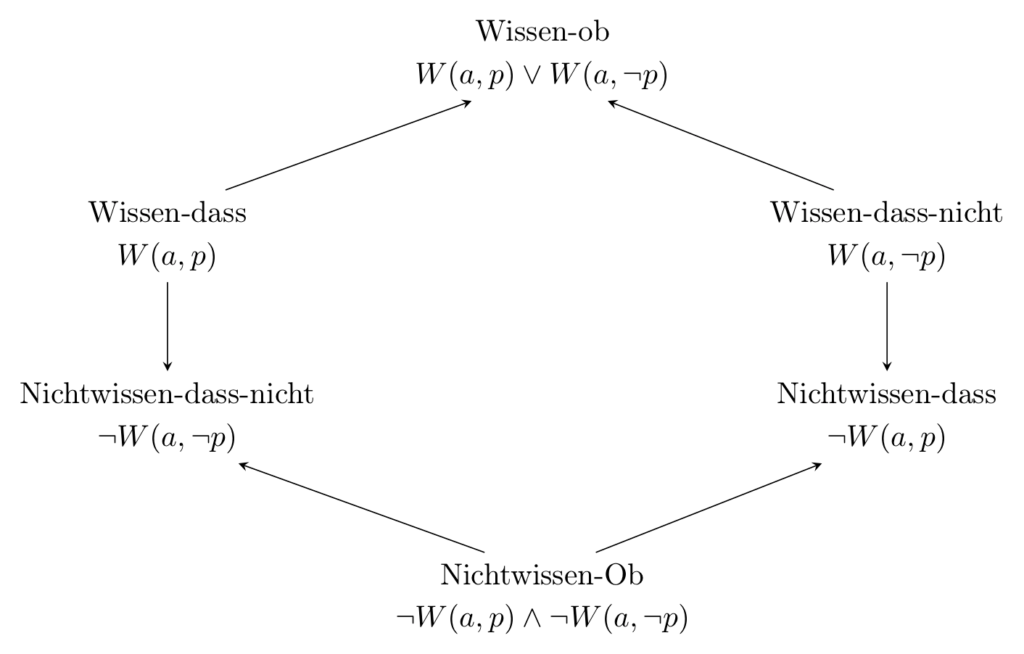
Setzt Nicht-Wissen Wahrheit voraus?
Im Rahmen des Themenschwerpunkts ‚Nicht-Wissen‘ soll nun insbesondere die sog. Negationsthese diskutiert werden, die von einem der Herausgeber (siehe den Beitrag „Die Wahrheit des Nichtwissens“ von Tim Kraft) wie folgt formuliert wird:
(N) „a ist nichtwissend, dass p, gdw. es nicht der Fall ist, dass a weiß, dass p“.
Diese Standardauffassung von ‚Nichtwissen‘ hält Kraft für eine logische Fiktion, wobei er auch auf Hintikka als Gewährsmann verweist. Betrachten wir dessen Bedenken also etwas ausführlicher! Hintikka erörtert (1962: 12-15) gewisse „Difficulties of translation“, d.h. Schwierigkeiten, die sich ergeben, wenn man die informellen Ausdrücke
- „a knows that p“
- „a knows whether p“
- „a does not know that p“
- „a does not know whether p“
- […]
- „It is possible, for all that a knows, that p“
durch Formeln seiner epistemischen Logik zu symbolisieren versucht. Für (1) wählt Hintikka selbstverständlich Kap, d.h. unsere A-Formel W(a,p). Ferner will Hintikka das in (2) erfasste ‚Wissen-ob‘ durch Kap ∨ Ka~p repräsentieren, was unserer U-Formel W(a,p)∨W(a,Øp) entspricht. Folgerichtig läuft (4), d.h. die Verneinung eines ‚Wissen-ob‘, auch für Hintikka darauf hinaus, dass a weder weiß, dass p, noch weiß, dass ¬p, so dass hier unsere Y-Formel ¬W(a,p) ∧ ¬W(a,¬p) resultiert. Ferner zeigen Hintikkas Ausführungen (1962: 43), dass der etwas merkwürdige Ausdruck (6) als äquivalent mit ~Ka~p, d.h. im Sinne unserer I-Formel ¬W(a,¬p) verstanden werden soll. Doch bei der Formalisierung von (3) glaubt Hintikka ein Problem erkannt zu haben. In gewisser Weise läge es seiner Auffassung nach zwar nahe, (3) als schlichte Negation ~Kap, d.h. im Sinne unserer O-Formel ¬W(a,p) zu verstehen. Aber, so Hintikka:
“a moment’s reflection shows that in some of
the most typical cases (3) is a correct form of words only if p is in
fact true. In such cases, (3) is not the contradictory of (1); it should rather
be translated as
(3)* „p & ~Kap.“”
Dieses Zitat ist gut geeignet, eine grundsätzliche Schwäche von Hintikkas Ansatz zu beleuchten: die unzureichende Unterscheidung zwischen den (semantischen) Wahrheitsbedingungen für das Vorliegen einer epistemischen Einstellung einerseits und den (pragmatischen) Bedingungen für die rationale Äußerbarkeit der entsprechenden Aussage andererseits.[2]
Ein konkretes Nicht-Wissen kann zwei ganz unterschiedliche Ursachen haben. Eine objektive Ursache liegt vor, wenn der fragliche Sachverhalt p überhaupt nicht besteht. Gemäß der Wahrheitsbedingung (W1) folgt ja aus ¬p unmittelbar ¬W(a,p). In einem solchen Fall wäre es jedoch absurd, a‘s Nicht-Wissen durch (3)*, also durch p ∧ ¬W(a,p) zu formalisieren, denn nach Voraussetzung ist p ja gerade nicht wahr, sondern falsch!
Eine subjektive Ursache des Nicht-Wissen liegt hingegen vor, wenn a gar nicht glaubt, dass p (bzw. stärker, wenn a sogar glaubt, dass nicht-p). Da gemäß (W2) ein Wissen, dass p, stets einen entsprechenden (starken) Glauben voraussetzt, folgt im Fall ¬G(a,p) unmittelbar ¬W(a,p). Ein solches subjektiv begründetes Nicht-Wissen ist aber logisch vollkommen unabhängig davon, ob der fragliche Sachverhalt p besteht oder nicht, d.h. ¬W(a,p) ist sowohl mit p als auch mit ¬p verträglich. Die durch Hintikkas Formel (3)* postulierte Wahrheit von p wäre also auch hier keineswegs gerechtfertigt.
Hintikkas Beobachtung, dass die korrekte Äußerung eines Satzes der Form ¬W(a,p) typischerweise voraussetzt, dass p der Fall ist, läuft im Grunde auf Folgendes hinaus. Im Gegensatz zur Aussage „a weiß nicht, ob seine Frau ihn betrügt“ gibt ein Sprecher (b) mit der Behauptung „a weiß nicht, dass seine Frau ihn betrügt“ dem Hörer gegenüber zu erkennen gibt, dass er selber (b) zu wissen glaubt, dass p. In diesem Sinne impliziert die letztere Äußerung pragmatisch, dass b die Wahrheit von p voraussetzt, auch wenn der Sachverhalt ‚a weiß nicht, dass p‘ semantisch keineswegs impliziert, dass p tatsächlich der Fall ist.
In Lenzen (1995) wurde gezeigt, wie man die Semantik und die Pragmatik epistemisch/doxastischer Aussagen in drei aufeinander aufbauenden Schritten entwickeln kann. Erstens sind – z.B. auf der Basis der obigen probabilistischen Interpretation – die Wahrheitsbedingungen für W(a,p), Ü(a,p) und G(a,p) zu erarbeiten, wobei es sich als sinnvoll erweist, auch „gemischte“ Einstellung der Art W(a,G(a,p)), G(a,W(a,p)), … in Betracht zu ziehen. Mit Hilfe der so gewonnenen Semantik kann man zweitens die allgemeine Theorie sprachlicher Implikaturen, wie sie P. Grice (1975) im Rahmen seiner Theorie der Kommunikation skizziert hat, hinreichend präzisieren. Drittens kann man die so gewonnenen pragmatischen Prinzipien auf die Äußerungen epistemisch/doxastischer Sätze anwenden und erhält u.a. folgende Resultate, bei denen das pragmatische Implizieren (im Gegensatz zum logischen Implizieren) mittels des Kunstwortes ‚implikieren‘ ausgedrückt wird.
1.1) Mit der Äußerung „b weiß, dass p“ implikiert der Sprecher a (≠b) nicht nur, dass er, a, davon überzeugt ist, dass b weiß, dass p, sondern auch, dass er selber davon überzeugt ist, dass p.
1.2) Mit der Äußerung „b weiß, ob p“ implikiert a, dass er davon überzeugt ist, dass b weiß, ob p. Er lässt es aber offen, ob er selber weiß, ob p, bzw. ob er eine (schwache oder feste) Meinung bezüglich p hat.
1.3) Mit der Äußerung „b weiß nicht, ob p“ implikiert a, dass er davon überzeugt ist, dass b nicht weiß, ob p. Er lässt es aber offen, ob er selber weiß, ob p, bzw. ob er eine (schwache oder feste) Meinung bezüglich p hat.
1.4) Mit der Äußerung „b weiß nicht, dass p“ implikiert a zum einen, dass er davon überzeugt ist, dass b nicht weiß, dass p; zum anderen implikiert er aber auch, dass er selber davon überzeugt ist, dass p.
In dem Spezialfall a=b, bei dem also der Sprecher Aussagen über seine eigenen epistemischen Zustände macht, ergibt sich:
2.1) Mit der Äußerung „Ich weiß, dass p“ implikiert der Sprecher a, dass er davon überzeugt ist, dass p. Die gleiche Implikation würde a aber auch mit der Äußerung ‚Ich bin mir ganz sicher, dass p‘ erreichen – ja sogar mit der schlichten Behauptung von p selber. Alle drei Äußerungen sind pragmatisch äquivalent, indem sie nicht mehr und nicht weniger zum Ausdruck bringen, als dass a davon überzeugt ist (bzw. zu wissen glaubt), dass p.
2.2) Mit der ziemlich ungewöhnlichen Äußerung „Ich weiß, ob p“ würde a implikieren, dass er eine feste Meinung bezüglich p hat, d.h. dass er entweder davon überzeugt ist, dass p, oder davon überzeugt, dass Øp. Eine solche Äußerung könnte man u.U. als Antwort auf die Frage eines anderen, b, gelten lassen, ob er, a, wisse, ob p. Diese Antwort bliebe aber unbefriedigend, weil b in aller Regel nicht nur wissen will, ob a weiß, ob p, sondern wissen bzw. erfahren will, ob p. Deshalb sollte die Äußerung „Ich weiß, ob p …“ noch näher spezifiziert werden, indem a entweder ergänzt: „…, nämlich p“ oder „…, nämlich ¬p“. Wenn a jedoch bereit ist, diese spezifische Information kundzutun, dann könnte er von vornherein einfacher antworten: „Ich weiß, dass p“ (bzw. „Ich weiß, dass ¬p“).
2.3) Mit der Äußerung „Ich weiß nicht, ob p“ implikiert a, dass er keine feste Meinung bezüglich p hat. Wenn a jedoch zumindest eine schwache Meinung bezüglich p hat, wäre es angebracht, die bloß negative Information „Ich weiß nicht, ob p“ um den Zusatz zu ergänzen: „…, aber ich glaube, dass p“ (bzw. „…, aber ich glaube, dass ¬p“).
2.4) Mit der sehr ungewöhnlichen Äußerung „Ich weiß nicht, dass p“ würde a zum einen implikieren, dass er davon überzeugt ist, dass er nicht weiß, dass p; zum anderen würde er (in Analogie zu 1.4) anscheinend implikieren, dass er davon überzeugt ist, dass p. Dies wäre jedoch ein epistemisch-logischer Widerspruch. Um diesen Widerspruch zu vermeiden, müsste a näher spezifizieren, wieso er nicht weiß, dass p. Einerseits wäre es möglich, dass (nach Meinung von a) das Nicht-Wissen die „objektive“ Ursache hat, dass p gar nicht der Fall ist; in einem solchen Fall wäre es aber angebracht, zu präzisieren: „…, im Gegenteil ich weiß, dass ¬p“. Andererseits könnte das Nicht-Wissen „subjektiv“ darin begründet sein, dass a nicht sicher ist, dass p; in diesem Fall sollte a entsprechend ergänzen: „…, denn ich glaube nicht, dass p“ bzw. „…, denn ich bin mir nicht sicher, dass p“.
Fazit
Wie in Lenzen (2020) ausführlicher gezeigt wird, lassen sich mit der hier skizzierten, auf einer präzisen Semantik beruhenden Pragmatik der epistemisch-doxastischen Begriffe nicht nur die Unklarheiten bzgl. der sog. Negationsthese beheben, sondern auch zahlreiche Probleme wie insbesondere Moores Paradox lösen.
Wolfgang Lenzen war bis zu seiner Pensionierung Professor für Analytische Philosophie an der Universität Osnabrück. Seine Forschungsschwerpunkte waren und sind: Wissenschaftstheorie, Epistemische Logik, Leibniz, Geschichte der Logik, Angewandte Ethik und Philosophie des Geistes. Daneben veröffentlichte er auch Bücher zum Ausdauersport und Bergsteigen. Als Pensionär fuhr er mit dem Fahrrad in einem Jahr um die Welt.
Literatur
Grice, Paul H. (1975): „Logic and Conversation“, in P. Cole & J. L. Morgan (eds.), Syntax and Semantics Vol. 3, New York: Academic Press, 41–58. Wiederabdruck in P. Grice, Studies in the Way of Words, Cambridge, MA (Harvard University Press) 1991, 22–40.
Hintikka, Jaakko (1962): Knowledge and Belief – An Introduction to the Logic of the Two Notions, Ithaca (Cornell University Press).
Lenzen, Wolfgang (1980): Glauben, Wissen und Wahrscheinlichkeit – Systeme der epistemischen Logik, Wien (Springer).
Lenzen, Wolfgang (1995): „On the Semantics and Pragmatics of Epistemic Attitudes”, in A. Laux & H. Wansing (eds.): Knowledge and Belief in Philosophy and Artificial Intelligence, Berlin (Akademie-Verlag), 181–197.
Lenzen, Wolfgang (2012): „How to Square Knowledge and Belief”, in J.-Y. Béziau & D. Jacquette (eds.), Around and Beyond the Square of Opposition, Basel (Birkhäuser), 305–311.
Lenzen, Wolfgang (2020): „Grice and Moore’s Paradox”, erscheint in: J. Brandl, B. Kobow & D. Messelken (Hrg.), Analytische Explikationen und Interventionen, Münster (mentis).
Parsons, Terence (2017): „The
Traditional Square of Opposition”, in: E. N. Zalta (ed.), The Stanford Encyclopedia of Philosophy (Summer 2017 Edition); https://plato.stanford.edu/archives/sum2017/entries/square/
[1] Da A und E konträr zueinander sind, folgt z.B. aus der Wahrheit von A die Falschheit von E, also (da I zu E kontradiktorisch ist) die Wahrheit von I.
[2] Hintikka kommt der Unterscheidung von Semantik und Pragmatik nur einmal ganz nahe, wenn er (1962: 113) im Zusammenhang der Erörterung der sog. KK-These, also der Frage, ob jedes Wissen, dass p, ein Wissen, dass man weiß, dass p, impliziert, ausführt: „In a sense, the expressions (63) [KaKap] and (64) [Kap] mean the same, but we have to distinguish what a form of words means [!] from what is meant by uttering them.“


